Summary
Introduced probability as the study of experiments and outcomes. Discussed sample spaces, events, the Fundamental Principle of Counting, permutations, and combinations. Covered unions and intersections of events, leading into the Inclusion-Exclusion Formula.
Probability is frequently the study of experiments, outcomes, and events.
Example
Experiment → Outcomes
- Rolling a die →
- Flipping a coin →
The collection of outcomes is called a sample space (), which can be finite or infinite. We will mostly concern ourselves with finite sample spaces in this course. A roll of a die has a finite sample space, while are infinite.
Definition
A probability on a sample space is a real number given to each possible outcome in a sample space, such that
The probability measure where all outcomes are equally likely is the uniform distribution. Each element has probability
Definition
An event is a subset of the sample space.
Intuitively, an event is a collection of outcomes.
Example
is an event with sample space .
Definition
The probability of an event is
Intuitively, we sum the probability of each event individually.
Example
Rolling two dice. .
Question
What is ?
Solution .
36, since there are 6 values for each coordinate, and
Problem
.
Example
Flip a coin three times. . .
- . .
Example
Flip a coin times. We don’t have a closed form for a general , but notice that .
For a general , a natural probability measure is the general uniform measure.
. , though is messy.
Counting
Theorem - Fundamental Principle of Counting
Suppose we have tasks and -th task can be done in ways.
Note
We assume every task does not affect any other task
Example
54-card deck. Place cards on table one by one. . We can do this in ways.
Definition
Given a positive integer , the factorial of is denoted
Note
Notice that represents the ways of reordering distinct objects. Additionally, counts the number of permutations of a set of numbers.
Example
A deck of cards takes
52!permutations. It’s unlikely that anyone in human history has ever shuffled a deck of cards the same way.
Corollary
n!counts the number of permutations of numbers
Example
Seating guests on chairs (). In how many ways can you do this?
Example
Select a set of chairs out of chairs. The difference here is order doesn’t matter.
The final example is a combination, where order doesn’t matter. The previous was the formula for a permutation, where order matters. The notation is also called ” choose ”, as we literally find all the ways of choosing elements from a set of .
Note
The binomial coefficient pops up in the binomial formula:
Note
Example
Toss a coin times. .
Example - Birthday Paradox
What is the probability that people were born on the same day?
The factorial ratio comes from counting “all birthdays distinct”: the first person has 365 choices, the second has 364, …, the -th has , so the count is . We divide by because there are total equally likely birthday assignments, then take to get “at least one match.”
In a similar light, the probability that someone in a group of people has the same birthday as you is:
Notice that it’s less likely someone will have the same birthday as you specifically compared to two arbitrary people sharing one.
Operations with Events
Recall that an event () is a subset of the sample space ().
Definition
Let be an event. .
Definition
Let be events.
- The union of is denoted by and contains all
- The intersection of is denoted by and contains all
We can write the probability of both of these notions.
Inclusion-Exclusion
This is called the inclusion-exclusion formula. We can make a weak claim from this principle, namely that
More generally (the union bound / Boole’s inequality), for events ,
What if we instead have 3 events? The inclusion-exclusion formula becomes
This simplifies as
Since we “over-subtracted” the center region, we need to add it back one more time.
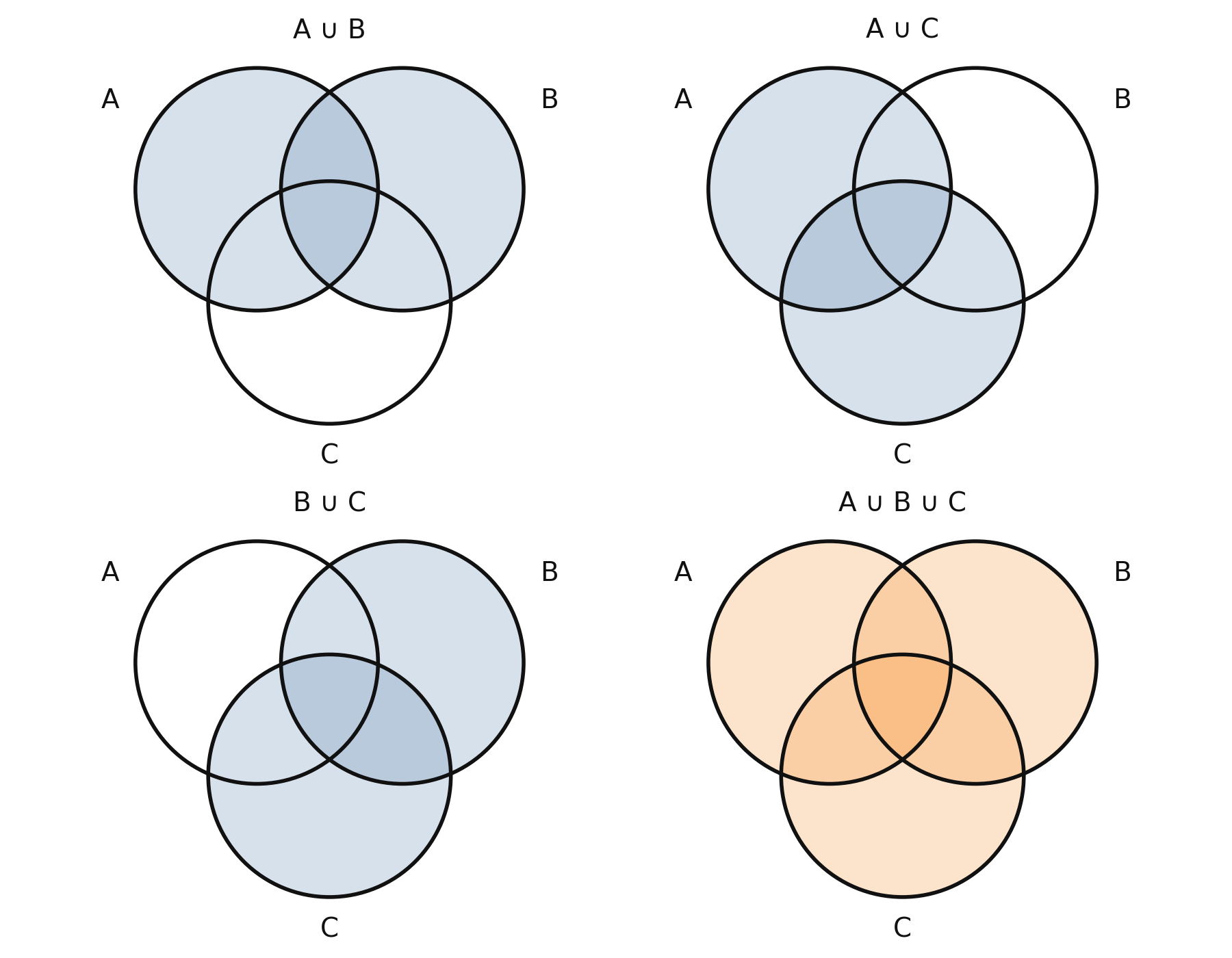
Definition
Generalized Inclusion-exclusion Formula For events ,
So for even cases, we subtract, and for odd cases, we add. We apply this in Conditional Probability & Independence to derive the law of total probability.